Recent Posts
Link
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
Tags
- 코루틴 빌더
- kotlin
- 오블완
- Kubernetes
- taint
- pytest
- 자원부족
- JanusWebRTCServer
- JanusWebRTC
- 코루틴 컨텍스트
- tolerated
- JanusWebRTCGateway
- k8s #kubernetes #쿠버네티스
- 깡돼후
- python
- terminal
- OptimisticLock
- PessimisticLock
- 헥사고날아키텍처 #육각형아키텍처 #유스케이스
- mp4fpsmod
- 겨울 부산
- k8s
- 개성국밥
- JanusGateway
- vfr video
- PersistenceContext
- Spring Batch
- 달인막창
- preemption #
- 티스토리챌린지
Archives
너와 나의 스토리
[Data Mining] Support Vector Machine (SVM) - Linearly Separble Classes 본문
Data Analysis/Data Mining
[Data Mining] Support Vector Machine (SVM) - Linearly Separble Classes
노는게제일좋아! 2020. 5. 16. 18:36반응형
Support Vector Machine(SVM)이란?
- 머신 러닝의 분야 중 하나로 패턴 인식, 자료 분석을 위한 지도 학습 모델
- 주로 분류와 회귀 분석(regression)을 위해 사용
- 두 카테고리 중 어느 하나에 속한 데이터의 집합이 주어졌을 때, SVM 알고리즘은 주어진 데이터 집합을 바탕으로 하여 새로운 데이터가 어느 카테고리에 속할지 판단하는 비확률적 이진 선형 분류 모델을 만든다.
정의
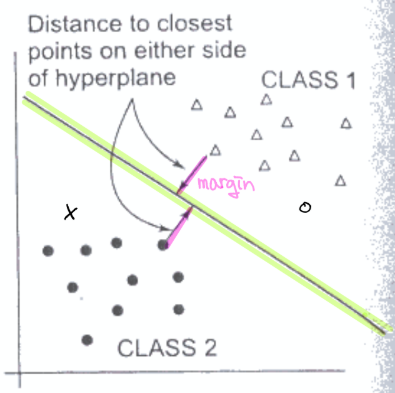
- hyperplane: 두 클래스를 나누는 것.
- 2차원 공간에 있는 데이터는 1차원(선) hyperplane으로 나눠지고, 3차원 공간에 있는 데이터는 2차원(평면) hyperplane으로 나눠진다.
- margin: hyperplane과 가장 가까운 곳에 위치한 데이터와의 거리
- SVM의 목표는 margin을 최대화하는 것이다.
- margin이 커야 새로운 데이터가 들어왔을 때 잘 분류할 수 있다.
Linearly Separble Classes
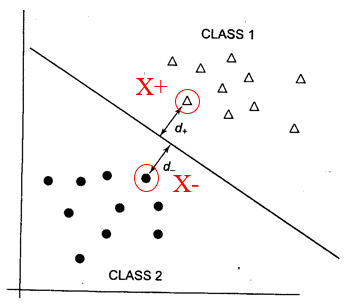
- 다음과 같이 두 클래스를 선형으로 나눌 수 있는 경우를 살펴보자.
- 각 클래스에서 hyperplane까지의 margin은 동일하다.
- 이 margin을 최대화하는 것이 SVM의 목적이다.
- X+: Positive space에서 hyperplane과 가장 가까운 데이터


- W·X+$w_0$ = 0 -> W·X - d = 0
- W: hyperplane의 법선 벡터(normal vector)
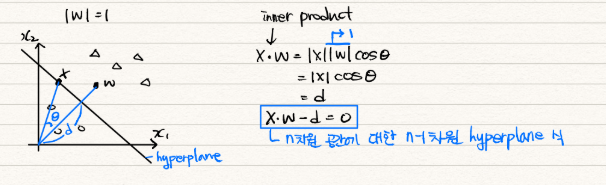
- $X^+$: $y_i$ = +1의 데이터 중에서 hyperplane과 가장 가까운 데이터 (support vector)
- $X^-$: $y_i$ = -1의 데이터 중에서 hyperplane과 가장 가까운 데이터 (support vector)
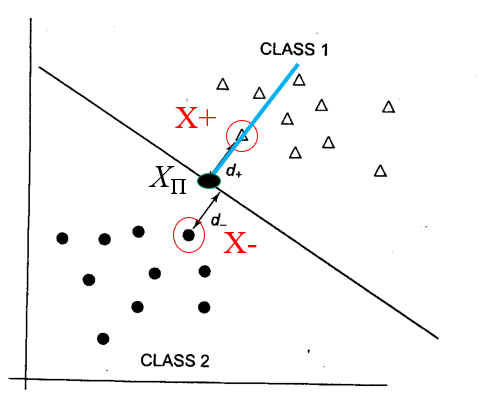
- 주어진 hyperplane과 같은 법선벡터를 가지면서 $X^+$를 지나는 초평면은 w·x-b = +1으로 나타낼 수 있다. $X^-$를 지나는 초평면은 w·x-b = -1으로 나타낼 수 있다.
- hyperplane의 margin: 각 서포트 벡터($X^+$, $X^-$) 사이의 거리
- 즉 margin = $\frac{2}{||w||}$
- SVM은 이 margin을 최대로 만드는 알고리즘이다.
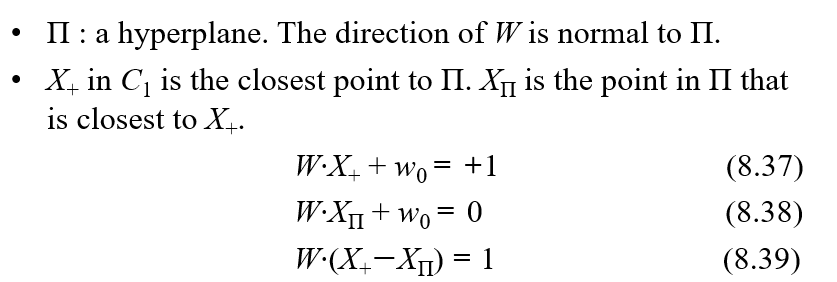


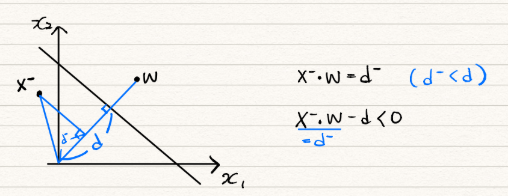
- unknown 데이터(X)를 넣어서 [X·W-d] 값이 음수이면 X는 W벡터와 반대쪽 클래스로 판단.
- 양수이면 X는 W 벡터와 동일한 쪽 클래스로 판단.
- Positive space 영역에 있는 데이터($y_i = +1$인 X_i)에 대해 w·$x_i$ - b ≥ +1
- Negative space 영역에 있는 데이터($y_i = -1$인 X_i)에 대해 w·$x_i$ - b ≤ -1
- 즉, $y_i(w·x_i - b) ≥ 1$, for all $1 ≤ i ≤ n$
- margin 위에 놓인 점들(support vectors)은 다음을 만족한다.
- $d_i(x_i·w+w_0)-1$ = 0
- $y_i(w·x_i - b) = 1$
Margin 최대화하기
- Margin = $\frac{2}{||W||}$
- 이를 최대화하려면 ||W||를 최소화하면 된다.
- 이는 $\frac{1}{2}{||W||}^2$를 최소화하는 것과도 동일하다.
- 최적화 문제: 제약 조건(constraints) $g(x)$에 따라 목적함수 최소화
- 목적 함수: $\frac{1}{2}{||W||}^2$
- 제약 조건($g(x)$): $d_i(X_i·W+W_0)-1 ≥0 i=1,...,Q
- 이 최적화 문제를 해결하기 위해 Lagrange Multipliers를 사용할 수 있다.
- Quadratic Programming 해법
Retrospect to Calculus "Lagrange Multiplier"
-
Lagrange Multipliers(라그랑주 승수법)을 이용하면 위의 문제를 다음과 같은 안장점을 찾는 문제로 나타낼 수 있다.
- g(x)=0 표면 위에 모든 점 중에서 f(P) 값이 최대 혹은 최소가 되는 점을 찾아라.
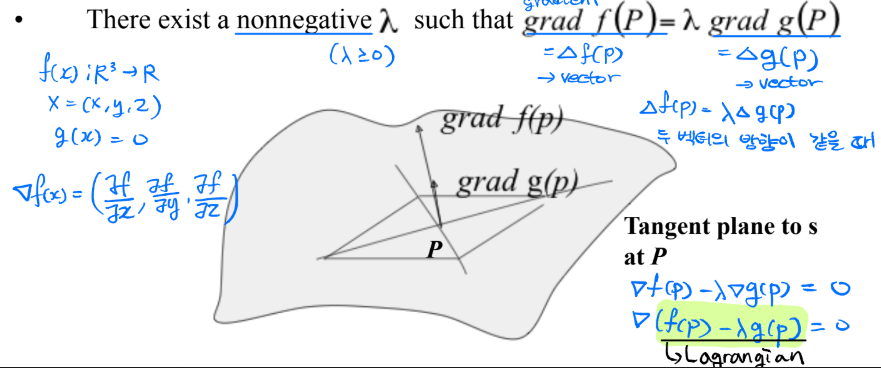
- Lagrangian = $f(x)-\lambda g(x)$
- f(x) = $\frac{1}{2}{||W||}^2$
- g(X) = $\sum^Q_{i=1}[d_i(X_i·W+w_0)-1]$
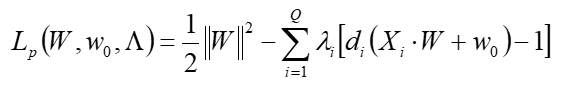
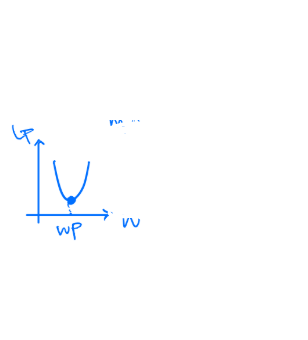
- minimizing $L_p w.r.t. W, w_0$ -> primal space
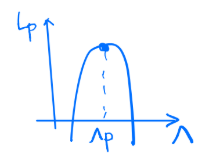

- maximizing $L_p$ w.r.t the non-negative $\lambda_i$ -> dual space
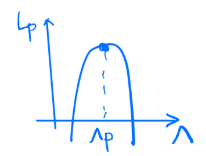

- Kühn-Tucker 조건은 만족되야 한다.
- Lagrange multiplier는 각 training data(x)에 대응되는 $\lambda$가 있다.
- Lagrange multiplier는 x가 support vector일 때만 0이 아니다.
- 즉, support vector일 때만, 신경써주면 됨


- 마지막 dual optimization 문제는 다음을 최대화하는 것!


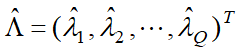
<- 이 중 support vector인 x에 대응되는 $\lambda$만 0이 아님(양수)



요약

참고 자료:
- 위키 백과: https://ko.wikipedia.org/wiki/%EC%84%9C%ED%8F%AC%ED%8A%B8_%EB%B2%A1%ED%84%B0_%EB%A8%B8%EC%8B%A0
반응형
'Data Analysis > Data Mining' 카테고리의 다른 글
Comments



