| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 | 29 |
| 30 | 31 |
- JanusWebRTCServer
- 겨울 부산
- 코루틴 빌더
- table not found
- JanusWebRTC
- Spring Batch
- JanusGateway
- PytestPluginManager
- 티스토리챌린지
- terminal
- pytest
- python
- 자원부족
- VARCHAR (1)
- kotlin
- JanusWebRTCGateway
- PersistenceContext
- mp4fpsmod
- taint
- 코루틴 컨텍스트
- vfr video
- 헥사고날아키텍처 #육각형아키텍처 #유스케이스
- 개성국밥
- 깡돼후
- 달인막창
- preemption #
- 오블완
- Value too long for column
- tolerated
- k8s #kubernetes #쿠버네티스
너와 나의 스토리
[Data Mining] CH8. Cluster Analysis: Basic Concepts and Algorithms 본문
[Data Mining] CH8. Cluster Analysis: Basic Concepts and Algorithms
노는게제일좋아! 2020. 6. 4. 01:05Cluster Analysis란?
- 서로 비슷한 것들을 묶는 것
- similar(or related)하면 같은 그룹
- Intra-cluster distances(cluster 내에서 거리)를 최소화
- different(or unrelated)하면 다른 그룹
- Inter-cluster distances(cluster간 거리) 최대화
- 특징:
- Unsupervised learning -> label이 없음
- 거리로 분석 -> feature간의 관계를 고려하지 않는다.
Type of Clusterings
- Clustering은 clusters의 집합
- Hierarchical clustering와 Partitional clustering을 구분하는 것은 중요하다.
- Partitional clustering:
- 각 데이터 객체는 정확히 하나의 부분집합에 포함되어야한다. 즉, 각 cluster들은 겹치면 안된다.
- Hierarchical clustering:
- Hierarchical tree로서 nested clusters의 집합이 구성된다.

Clustering 간의 다른 차이들
- Exclusive vs Non-exclusive
- Exclusive: 한 데이터는 하나의 cluster에만 속함.
- Non-exclusive: 어떤 데이터는 여러개의 그룹에 속할 수 있음
- Fuzzy vs Non-fuzzy
- Fuzzy clustering: 한 데이터는 모든 cluster에 [0,1] 사이의 weight(확률)을 가지고 속하게 된다.
- 어떤 데이터가 A 그룹에 속할 확률 ?, B 그룹에 속할 확률 ? 이런 식
- Fuzzy clustering: 한 데이터는 모든 cluster에 [0,1] 사이의 weight(확률)을 가지고 속하게 된다.
- Partial vs complete
- 일부 데이터에 대해서만 clustering할 수도 있다.
- Heterogeneous vs Homogeneous
Types of Clusters: Center-Based
- Centroid: cluster의 중심, cluster에 있는 점들의 평균 -> cluster 내의 데이터들의 평균 or 위치적 중심 영역
- Medoid: cluster에서 대표적인 데이터(point) -> cluster 내에 중간쯤에 위치한 '데이터'
Types of Clusters: Contiguity-Based
- 가장 가까운 이웃
- ㅁ-ㅁ-ㅁ-ㅁ 이런식으로 데이터가 있을 때, 양 끝의 데이터는 서로 멀지만, 바로 옆 데이터와는 가깝기 때문에 점점 연결됨

Types of Clusters: Density-Based
- points 영역의 밀도가 높은 것을 cluster로 둔다.

Types of Clusters: Objective Function
- Cluters는 목적 함수로 정의된다.
- 목적 함수 예: cluster 내의 데이터들 사이간 거리 or cluster 사이간 거리
- NP Hard: 데이터들을 가능한 모든 방법으로 분리
- 넘나 expensive
- global 또는 local objectives를 가질 수 있다.
- Hierarchical clustering 알고리즘은 전형적으로 local objectives이다.
- Partitional 알고리즘은 전형적인 global objectives
- Proximity matrix: weighted grah 정의 -> weighted: similarity or dissimilarity
- Clustering은 요소들을 연결한 그래프를 분리하는 것과 같다.
Clustering Algorithm
- K-means and its variants
- Hierarchical clustering
- Density-based clustering
K-means Clustering
- 랜덤하게 k개의 points를 뽑고, 이를 각 cluster의 centroid로 둔다.
- 각 데이터들을 이 K개의 centroid 중 가장 가까운 cluster에 할당한다.

- 상대적으로 소수의 데이터만 변화할 때까지 반복하다가 종료
- k-means는 수렴 보장된다.
- 복잡도: O(n*K*l*d)
- n: #point, K: #cluster, I: #iteration, d: #attribute
K-means Clusters 평가:
- 보통 SSE(Seum of Squared Error)로 측정
- 각 point에 대해 가장 가까운 cluster와의 거리를 에러로 둔다.
- x: cluster Ci에 있는 point, mi: medoid

Problems with selecting initial points
- k개의 points를 뽑을 때, 이 points가 k개의 cluster에 각각 속하는 데이터일 확률은 적다.
- 특히, k개 크고, 각 cluster의 사이즈가 서로 비슷할 때, 확률은 더 작아진다.
- 만약, cluster 수가 k이고, 각 cluster 내에 포함된 points 수가 n일 때,

Solutions to initial centroids problem
- 여러번 돌려서, 그 중 좋은걸 뽑기
- 도움은 되지만, 확률은 우리편이 아니다 ㅎㅎ
- initial centroid를 결정하기 위해 hierarchical clustering 하기
- initial centroid를 k개 이상 뽑고, 이 중에서 제일 계산 결과가 좋은 것 k개를 고르기
- Postprocessing
- Bisecting K-means
- 계속 cluster를 이등분 해나감
- 초기화 문제에 그다지 민감하지 않음
Empty Clusters 처리
- SEE가 가장 높은 cluster에서, SSE에 가장 많이 기여한(중심에서 가장 먼) 데이터를 골라서 분리
Updating Centers Incrementally
- 기본 K-means 알고리즘에서, centroids는 모든 데이터들이 각 centroid로 할당된 후 업데이트하기
- 단점:
- centroids를 뽑고 각 cluster 계산하다가 중간에 centroid를 이동시키는 것은 cost가 크다.
- 계산 순서에 따라 결과가 달라질 수 있다.
- 장점:
- empty cluster가 생기지 않는다.
- weight를 줘서 영향을 변화시킬 수 있다.
Pre-processing and Post-processing
- Pre-processing
- data를 normalize
- outliers를 제거
- Post-processing
- outliers를 나타내는 작은 clusters를 제거
- 'loose'한(상대적으로 SSE가 높은) clusters를 쪼개기
- 상대적으로 SSE가 낮은 clusters를 merge
Bisecting K-means
- SSE가 제일 높은 Cluster를 둘로 나눔

K-means의 한계
- cluster들끼리 크기, 밀도, 모양이 다를 때 문제가 생긴다.
- 데이터가 outliers를 포함할 때 문제가 생긴다.
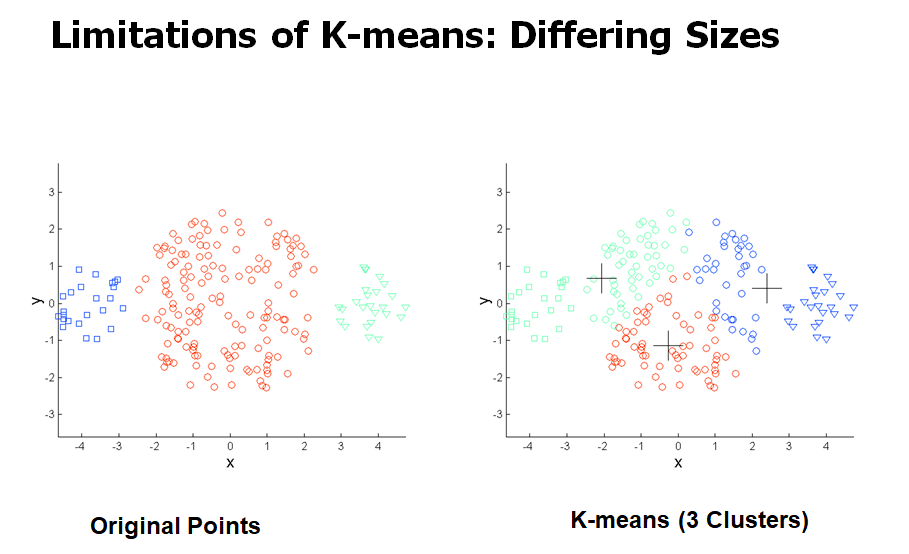
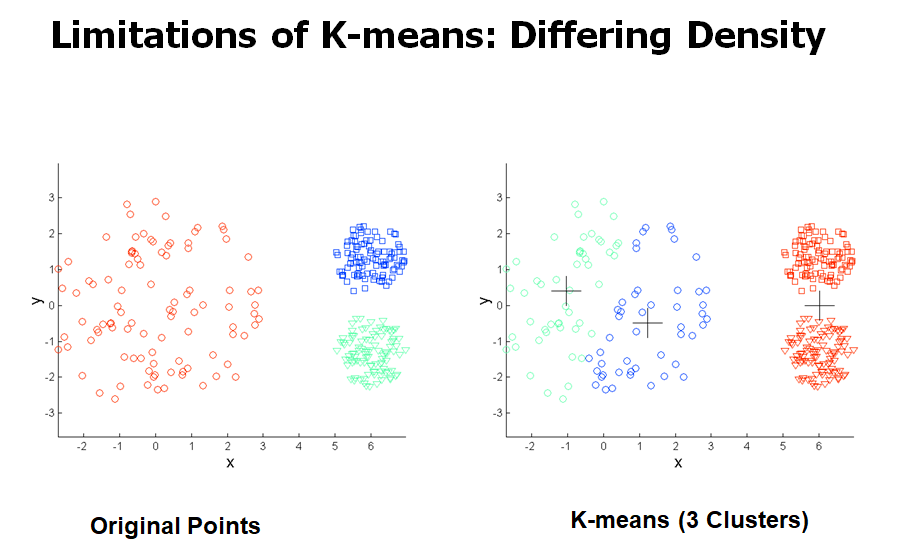
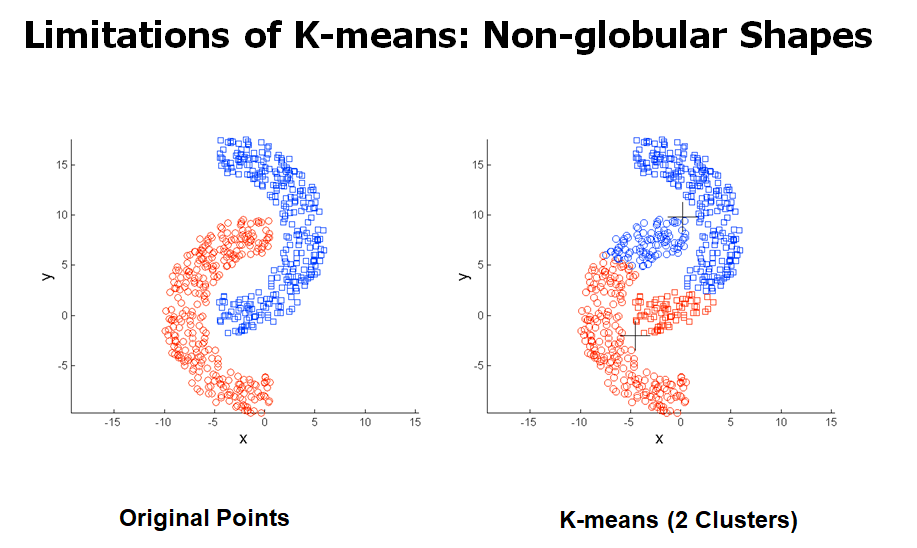
K-means의 한계 극복하기
- clusters를 많이 찾아서 merge
Hierarchical Clustering
- nested cluster를 hierarchical tree로 구성

- 장점:
- clusters의 개수 지정 안하고 hierarchical tree 구성하고, 원하는 cluster 개수만큼 나누면 된다.
- hierarchical clustering의 주요 유형
- Agglomerative: Bottom-up 방식
- 각각의 모든 점을 cluster로 시작 -> 즉, 처음에는 n개의 clusters가 존재
- 각 step에서, 가장 가까운 clusters 쌍을 merge
- 하나의 cluster만 남을 때까지 진행
- Divisive: Top-dowm 방식
- 하나의 cluster로 시작 -> 즉, 처음에는 모든 점들이 하나의 cluster에 포함됨
- 각 step에서, 각 cluster에 point가 하나만 남거나, k개의 clusters만 남을 때까지 split
- Agglomerative: Bottom-up 방식
Agglomerative clustering algorithm
- 이게 더 유명한 hierarchical clustering 기술임
- 기본 알고리즘:
1. proximity matrix 계산
2. 각 points를 cluster에 할당
3. Repeat
4. 두 개의 가까운 clusters 쌍을 merge
5. proximity matrix를 update
6. Untile
7. 하나의 cluster만 남을 때까지 - proximity of two clusters에 대한 정의는 애플리케이션마다 다름
- merge하고, 이것과 연관 있는 cluster들에 대한 proximity matrix 업데이트하면됨.
- ex) c2와 c5를 merge 했다면, 밑에 그림에서 색칠된 부분만 update 해주면 된다.

Inter-Cluster Similarity를 어떻게 정의할까?

1. Min
- 각 cluster에서 가장 가까운 점끼리 거리 구함

2. Max
- 각 cluster에서 가장 먼 점끼리 거리 구함

3. Grop Average
- NxM개의 모든 경우의 평균

4. Distance Between Centroids
- 한 cluster 내에서 점들의 x값, y값을 각각 평균내서 centroid를 구함
- 각 cluster의 centroid 점끼리의 거리 구함
Cluster Similarity: Min or Single Link
- similarity가 가장 높은 pair끼리 묶음
- matrix 대칭이므로 색칠된 부분만 보면된다.

- 장점:
- 타원형 아닌 모양도 핸들링할 수 있다.
- 단점:
- noise랑 outliers에 민감
Cluster Similarity: Max or Complete Linkage
- 현재 (1,2) (4,5) (3)로 cluster가 구성되있는 상황일 때,
- (1,2) (4,5) 두 cluster 중 3과 merge될 cluster를 찾아야한다.
- (1,3)=0.1 (2,3)=0.7 이니까 (1,2)와 3과의 similariry는 둘 중 0.1을 선택한다.
- distance가 가장 먼 것 = similarity가 가장 작은 것
- (4,5)도 마찬가지로 0.3을 선택


- 장점:
- noise와 outliers에 덜 민감
- 단점:
- 큰 cluster를 분리하는 경향이 있다.
- 둥글둥글하게 cluster가 이루어지는 경향이 있다.
Cluster Similarity: Group Average
- 두 cluster의 proximity = 서로 다른 cluster의 points들과의 거리의 평균

- Single과 Complete link의 절충안
- 장점:
- noise와 outliers에 덜 민감
- 단점:
- 둥글둥글하게 cluster를 형성하는 경향이 있다.
Cluster Similarity: Ward's Method
- Similarity: 두 개의 clusters를 merge할 때, SSE의 증가(△SSE)
- △SSE가 가장 작은 pair 선택해서 merge
- 두 Cluster가 merge하면 SSE가 업데이트됨
- 장점:
- noise와 outliers에 덜 민감
- 단점:
- 둥글둥글한 모양으로 형성되는 경향이 있다.
<연산량>
MIN, MAX < Group Average < Ward's Method
Hierarchical Clustering: Time and Space requirements
- proximity matrix 형성하는데 O(N2)의 공간 복잡도가 필요
- 한 번 연산할 때마다, proximity matrix의 사이즈는 1씩 준다.
- 0. NxN
- 1. (N-1)x(N-1)
- 2. (N-2)x(N-2)
- 총 시간 복잡도는 O(N3) = N2+(N−1)2+(N−2)+...
- O($N^2log(N))까지 시간 복잡도 줄일 수 있음
Hierarchical Clustering: 문제와 한계점
- 일단 두 개의 clusters를 merge하면, 되돌릴 수 없다.
- 목적함수를 직접적으로 최소화할 수 없다.
- global minimize 안됨
- 다른 스키마를 가지면, 다음과 같은 문제가 생길 수 있다:
- noise와 outliers에 민감
- 크기가 다른 clusters나 볼록한 모양을 다루기 힘들다
- 큰 cluster를 분리시켜야 한다.
MST: Divisive Hierarchical Clustering
- 각 데이터들을 MST(Minimum spanning Tree)로 build
- edge를 없앰으로써 새로운 cluster를 만듦


DBSCAN
- DBSCAN: 밀도 기반 알고리즘
- 밀도: 지정한 radius(Eps) 내에 있는 점들의 수
- core point: 어떤 cluters의 중심으로 거리(Eps) 내에 있는 점들의 개수가 MinPts가 넘는 경우, 그 중심을 core point라고 한다.
- border point: core point에 해당되는 cluster 경계에 있는 점
- noise point: core point도 border point도 아닌 점





