Recent Posts
Link
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |||
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 |
Tags
- 코루틴 빌더
- 개성국밥
- table not found
- preemption #
- JanusWebRTCServer
- VARCHAR (1)
- 오블완
- Value too long for column
- 달인막창
- python
- JanusGateway
- vfr video
- 자원부족
- mp4fpsmod
- 티스토리챌린지
- pytest
- k8s #kubernetes #쿠버네티스
- Spring Batch
- 헥사고날아키텍처 #육각형아키텍처 #유스케이스
- JanusWebRTC
- JanusWebRTCGateway
- 코루틴 컨텍스트
- terminal
- tolerated
- PersistenceContext
- PytestPluginManager
- 겨울 부산
- kotlin
- taint
- 깡돼후
Archives
너와 나의 스토리
[Data Mining] CH9. Cluster Analysis: Advanced Concepts and Algorithms 본문
Data Analysis/Data Mining
[Data Mining] CH9. Cluster Analysis: Advanced Concepts and Algorithms
노는게제일좋아! 2020. 6. 4. 12:12반응형
Distance betwwen clusters
- Single link: MIN distance로 구하기
- Complete link: MAX distance로 구하기
- Average: 모든 점들 사이(각 cluster간) 거리 평균
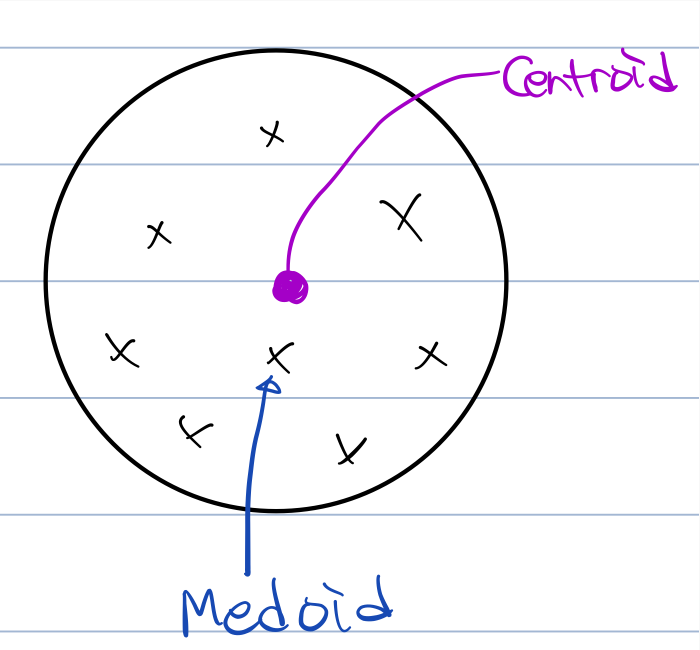
- Centroid: 각 cluster의 centroid끼리 거리 구함
- Medoid: 각 cluster의 medoid끼리 거리 구함
- 반드시 데이터이여야 함.
- Centroid ≠ Medoid
- Cenroid (Cm): cluster 중심
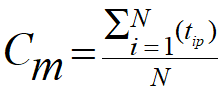
- Radius (Rm): centroid와 각 점들(해당 cluster 내의) 사이의 거리 제곱의 평균
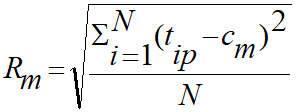
- Diameter (Dm): cluster 내의 모든 점 사이(모든 pair) 거리 제곱의 평균
- A->B, B->A 둘 다 카운트 하니까 n(n-1)로만 나눠줌
- fully connected graph에서 vertex 개수가 n개 일 때, edge 수는 n(n-1)/2 개이다.
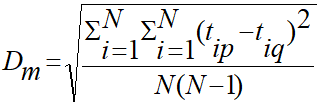
BIRCH (Balanced Iterative Reducing and Clustering Using Hierarchies)
- Incrementally하게 CF(Clustering Feature) tree와 hierarchical data 구조를 구성
- 단계 1: DB를 스캔해서 메모리 안에 CF tree 만들기
- 단계 2: 임의의 clustering 알고리즘 사용해서 CF-tree의 leaf node를 cluster
- 장점: 한 번의 스캔으로 clustering 잘할 수 있음
- 단점: 숫자 데이터만 다룰 수 있음, 레코드 순서에 민감
Clustering Feature Vector in BIRCH
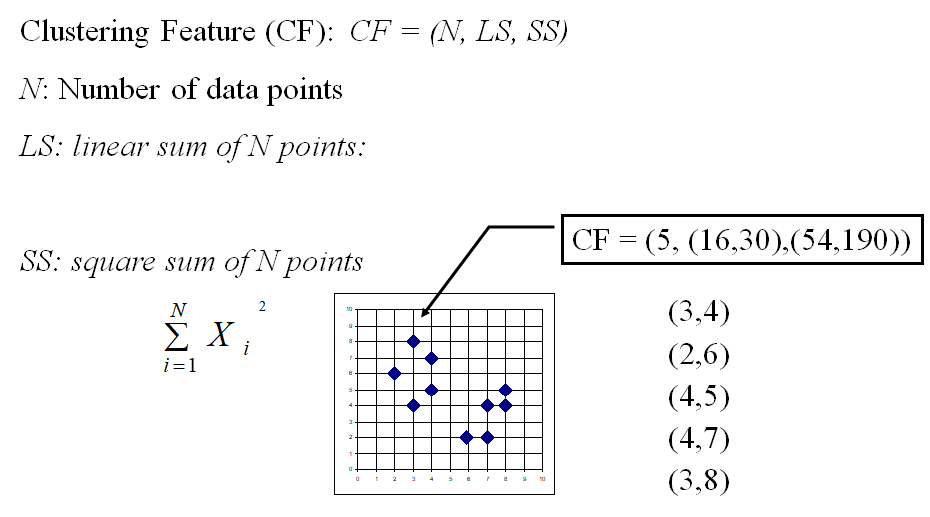
LS=(x 값의 평균, y 값의 평균)
SS=(x 값 제곱의 평균, y 값 제곱의 평균)
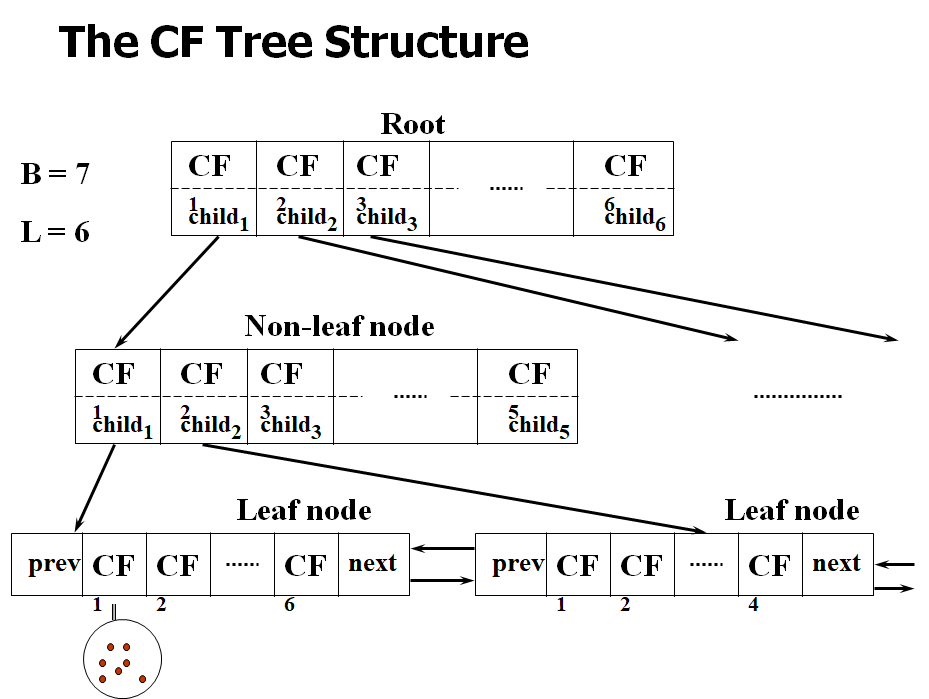
CF-tree in BIRCH
- CF tree는 height-balanced tree이다.
- CF tree는 두 개의 파라미터를 가진다
- Branching factor: max # of children
- Threshold: max diameter of sub-cluster를 leaf node에 저장 (cluster 크기 조절)
The Birch Algorithmd
- Cluster Diameter
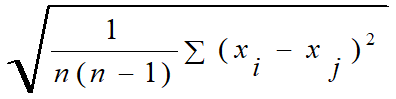
- 입력 데이터의 각 point에서
- 가까운 leaf entry 찾기
- leaf entry에 point 추가하고 CF 업데이트
- 만약 entry diameter > max_diameter이면 leaf를 쪼갠다.
- 알고리즘 시간 복잡도: O(n)
- 걱정:
- 데이터 삽입 순서에 민감
- leaf node의 크기를 고정하기 때문에, cluster가 자연스럽지 않을 수 있다.
- cluster가 둥근 형태로 제한될 수 있다.
Hierarchical clustering: 다시보기
- Nested clusters 만듦
- Agllomerative clustering 알고리즘은 proximity를 어떻게 정의하는지에 따라 다양하다
- MIN(Single link) - noise/outliers에 민감
- MAX/Group avearge - 둥근 모양이 아닌 형태의 cluster에서는 잘 작동 안 함
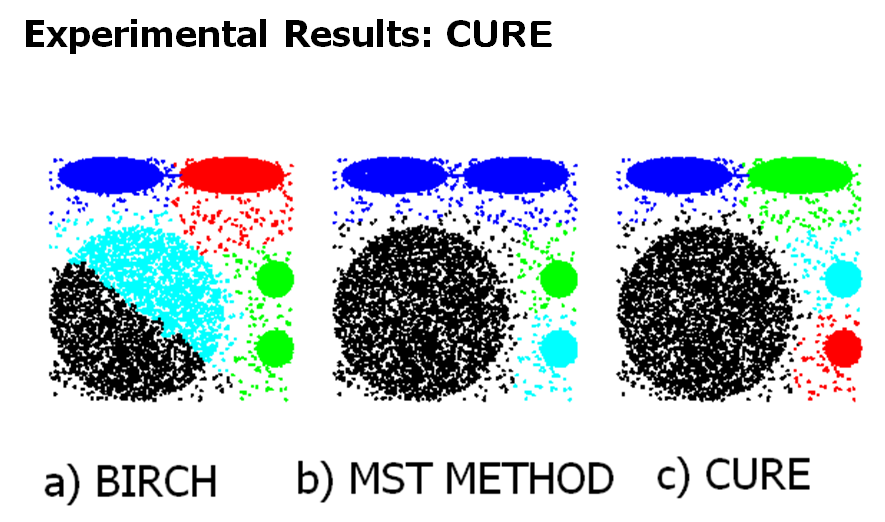
- CURE 알고리즘 -> 두 문제 다 해결 가능
- 주로 그래프 기반 알고리즘 형태로 시작
CURE: Another hierarchical approach

- 각 cluster에서 몇 개의 점만 대표로 뽑고, centroid 쪽으로 이동시킴 -> shrinking
- 이 때, 대표 points 수는 상수로 고정
- shirinking -> noise/outliers 문제를 예방할 수 있다.
- cluster similarity는 다른 cluster의 대표 points와 해당 cluster의 대표 points와의 similarity
- 장점:
- shirinking을 통해 noise/outliers 문제 예방
- CURE는 임의의 모양과 크기의 clusters를 잘 다룰 수 있다.
- 단점:
- cluster 간의 밀도가 다르면 잘 다루지 못 함
그래프 기반 clustering
- proximity graph를 사용해 graph-based clustering을 수행한다.
- 처음: proximity graph를 fully connected로 초기화
- 각 edge는 weight를 가짐
- 그리고 점점 cluster를 쪼갬
- clusters를 그래프의 connected components로 보면 됨.
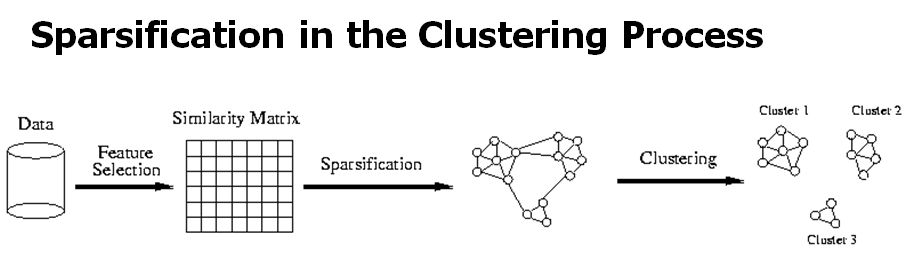
- Sparsification
- distance가 threshold 이상인 edge를 제거
- aproximity matrix에서 99%가 제거됨
- 데이터 clustering하는 데 드는 시간 절약
- 핸들링할 수 있는 문제 크기 증가
- sparsification 기술은 1%만의 연결(nearest neighbors)만 가짐
- cluster간의 거리를 명확하게 해줌으로써 noise/outlier 영향을 줄임
- distance가 threshold 이상인 edge를 제거
Chameleon: Clustering using dynamic modeling
- 데이터 셋의 특성에 적응해 자연스러운 clusters를 찾음
- clusters 간의 similarity를 측정하기 위해 dynamic model을 사용
- Main property: relative closeness & relative inter-connectiviy of the cluster
- 결과 클러스터가 구성 클러스터와 특정 속성을 공유하는 경우 두 클러스트를 결합함.
- merging scheme는 self-similarity를 보존한다.
Chameleon: Steps
- Preprocessing step:
- 데이터를 그래프로 표현
- K-NN(K-nearest-neighbor) 그래프 구성
- 데이터를 그래프로 표현
- 단계 1:
- multilevel graph partitioning 알고리즘을 사용하여 잘 연결된 정점으로 구성된 다수의 클러스터를 찾는다.
- 단계 2:
- hierarchical agglomerative clustrering을 사용해서 sub-clusters를 merge
- 공유하는 특성이 있으면 merge
- Two key properties:
- Relative Interconnectivity: cluster 내 connection
- Relative Closeness: 두 clusters 간 절대적 closeness
- hierarchical agglomerative clustrering을 사용해서 sub-clusters를 merge
끝
반응형
'Data Analysis > Data Mining' 카테고리의 다른 글
| [Data Mining] Dimensionality Reduction 다차원 척도법 (0) | 2020.06.28 |
|---|---|
| [Data Mining] Genetic Algorithm 유전 알고리즘 / 퀴즈 (0) | 2020.06.26 |
| [Data Mining] CH8. Cluster Analysis: Basic Concepts and Algorithms (0) | 2020.06.04 |
| [Data Mining] Support Vector Machine (SVM) - Non-linearly Separable Data (2) | 2020.05.16 |
| [Data Mining] Support Vector Machine (SVM) - Linearly Separble Classes (0) | 2020.05.16 |
Comments




