Recent Posts
Link
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |||
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 |
Tags
- 코루틴 빌더
- 오블완
- 자원부족
- JanusWebRTCGateway
- VARCHAR (1)
- pytest
- terminal
- Value too long for column
- mp4fpsmod
- JanusGateway
- JanusWebRTC
- JanusWebRTCServer
- Spring Batch
- 깡돼후
- 코루틴 컨텍스트
- taint
- kotlin
- PytestPluginManager
- 티스토리챌린지
- python
- 개성국밥
- 헥사고날아키텍처 #육각형아키텍처 #유스케이스
- table not found
- 겨울 부산
- preemption #
- 달인막창
- PersistenceContext
- k8s #kubernetes #쿠버네티스
- vfr video
- tolerated
Archives
너와 나의 스토리
[컴퓨터 보안] 정수론 기초 - Divisibiliy, GCD, Congruences, Modular, 역원 본문
Computer Security
[컴퓨터 보안] 정수론 기초 - Divisibiliy, GCD, Congruences, Modular, 역원
노는게제일좋아! 2020. 10. 22. 14:33반응형
Divisibility
- a|b
- a는 b의 약수
- b÷a의 나머지는 0
- ex) 13|182
- 특징
- a|1이면 -> a=±1
- a|b이고 b|a이면 -> a=±b
- b!=0인 모든 b는 0을 나눔
- a|b이고 b|c이면 -> a|c
- b|g이고 b|h이면 -> b|(mg+nh)
GCD(Greatest Common Divisor)
- a, b의 최대 공약수
- gcd(a, b)로 표현
- [gcd(0, 0) = 0]으로 정의
- gcd(a, b) =c
- c는 양의 정수
- c는 a와 b의 약수
- a와 b의 모든 약수는 c의 약수
Congruences
- (a mod n) = (b mod n)인 경우 두 정수 a, b를 "congruent modulo n"이라고 한다.
- 표현: a ≡ b (mod n)
- a ≡ 0 (mod n)이면 n|a이다.
- 특징
- a ≡ b (mod n)는 n|(a-b)이다.
- a ≡ b (mod n)이면 b ≡ a (mod n)
- a ≡ b (mod n)이고 b ≡ c (mod n)이면 a ≡ c (mod n)
Modular Arithmetic
- [(a mod n) + (b mod n)] mod n = (a+b) mod n
- [(a mod n) - (b mod n)] mod n = (a-b) mod n
- [(a mod n) * (b mod n)] mod n = (a*b) mod n
Modular inverse(모듈러 역원)
- a의 역원은 $a^{-1}$
- a*$a^{-1}$=1
- 모듈러 역원
- a (mod n)의 역원은 $a^{-1}$이다.
- 즉, a*b (mod n) =1을 성립하는 b는 a의 역원이다.
- 이 역원은 a와 n이 서로소인 경우에만 존재한다.
* a + 0 = a -> 0은 덧셈에 대한 항등원
* a*1 = a -> 1은 곱셈에 대한 항등원
* a와 b를 연산한 결과가 항등원이 될 때, b를 a의 역원이라고 한다.
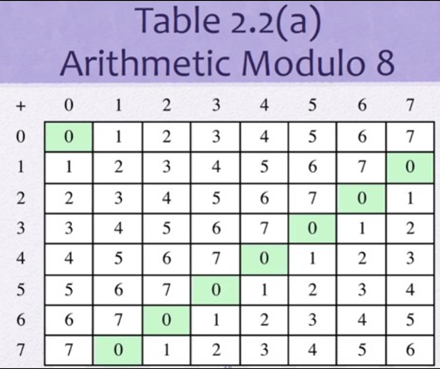
- (mod n)에 대해 나올 수 있는 수의 범위는 [0, (n-1)]이다.
- n이 8이라고 할 때, 가능한 모든 값을 서로 더한 것(mod n)을 표로 나타내면 좌측의 그림과 같다.
- 즉, (mod n)에 대해 [0, (n-1)]끼리의 덧셈에 대해 역원이 항상 존재한다.
- 0: 항등원
- a+x=0
- 즉, a에 어떤 값을 더해서 그 결과가 항등원(0)이 되도록 하는 x를 역원이라고 한다.
- ex) (mod 8)일 때, 3의 역원은 5
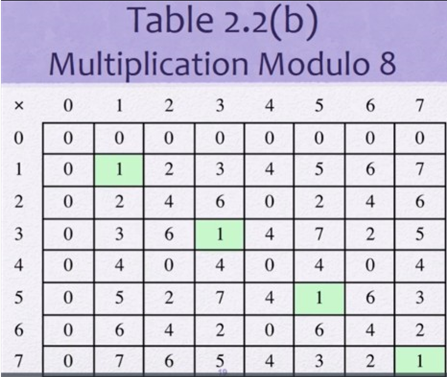
- 1: 곱셈에 대한 항등원
- a*x=1을 성립하는 x를 a의 역원이라고 함.
- 여기서 2의 경우 (mod 8)에 대한 역원을 가질 수 없음
- ㄴ 어떤 값을 곱해도 홀수가 될 수 없으므로
- (mod n) 연산에 대해 곱셈에 대한 역원이 존재하려면 a와 n가 서로소이어야 한다.
- a와 b가 서로소 -> gcd(a,b)=1
- 예: a=3 n=8이라면, gcd(3, 8)=1로 a, n은 서로소이다.
- 그렇다면, a*a mod 8은 1로 역원을 가지게 된다.

* Z: 모든 정수의 집합
* $Z_n$: n으로 나눴을 때 모든 나머지들의 집합 {0, ..., n-1}
* 덧셈의 역원은 항상 존재. But, 곱셈의 역원은 상황에 따라 다름.
역원을 구하는 방법
- 덧셈의 역원 구하기
- -1 곱하면 됨
- ex) 3의 역원은 -3
- -3 (mod 8) = 5
- 곱셈의 역원 구하기
- 가장 많이 쓰이는 방법 -> Extended Euclidean Algorithm
출처:
- [Cryptography and Network Security: Principles and Practices]
반응형
'Computer Security' 카테고리의 다른 글
| Group, Finite Fields, Polynomial GCD, 다항식을 bit string으로 계산 (0) | 2020.10.23 |
|---|---|
| 페르마(Fermat), 오일러(Euler) 정리 / Primality test - Miller-Rabin Algorithm 설명 및 Python 코드 구현 (4) | 2020.10.23 |
| 역원 구하기 - Euclidean Algorithm / Extended Euclidean Algorithm (0) | 2020.10.22 |
| [컴퓨터 공학] 용어 설명 및 최근 경향 - EPP/EDR/AI (0) | 2020.09.28 |
| Web Hacking (0) | 2020.09.25 |
Comments



