Recent Posts
Link
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |||
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 |
Tags
- PersistenceContext
- addhooks
- Value too long for column
- JanusWebRTCGateway
- taint
- PytestPluginManager
- JanusGateway
- pytest
- VARCHAR (1)
- JanusWebRTCServer
- 코루틴 빌더
- 겨울 부산
- JanusWebRTC
- vfr video
- tolerated
- 티스토리챌린지
- terminal
- 달인막창
- 코루틴 컨텍스트
- 깡돼후
- 자원부족
- table not found
- 개성국밥
- mp4fpsmod
- 헥사고날아키텍처 #육각형아키텍처 #유스케이스
- kotlin
- Spring Batch
- 오블완
- python
- preemption #
Archives
너와 나의 스토리
페르마(Fermat), 오일러(Euler) 정리 / Primality test - Miller-Rabin Algorithm 설명 및 Python 코드 구현 본문
Computer Security
페르마(Fermat), 오일러(Euler) 정리 / Primality test - Miller-Rabin Algorithm 설명 및 Python 코드 구현
노는게제일좋아! 2020. 10. 23. 00:37반응형
* 해당 글의 최하단에 Miller-Robin test 설명이 요약되어있습니다.
Prime Number(소수)
- : 1과 자기 자신으로만 나눠지는 수
- number theory에서 중요한 역할
- 1보다 큰 모든 정수는 소수의 거듭제곱의 곱으로 유일하게 표현 가능하다.
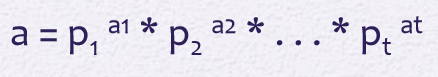
Fermat's Theorem(페르마 정리)
- [p: 소수, a: p로 나눠지지 않는 양의 정수]라면
- $a^{p-1}$ ≡ 1 (mod p)
- [p: 소수, a: 양의 정수]라면
- $a^{p}$ ≡ a (mod p)
- 위 식은 a가 p로 나눠지는지더라도 성립
Euler's Theorem(오일러 정리)
Euler totien function ϕ(n)
- ϕ(n): 1부터 n까지의 양의 정수 중에 n과 서로소인 것의 개수
- n이 두 소수의 곱이라면 -> n = p*q
- ϕ(n) = (p-1)(q-1)
- ϕ(p) = p-1
- ex) 15=3*5
- ϕ(15) = 2*4 =8
Euler's Theorem
- a와 n이 서로소일 때, 성립하는 식:
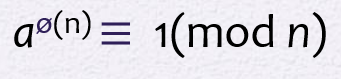
- a와 n이 서로소가 아니여도 성립하는 식:
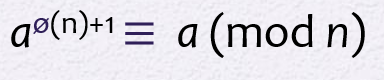
Primality test
- : 어떤 자연수 n이 소수인지 합성수인지 판별하는 알고리즘
- 방법 1: Trial division
- 범위 [2, $\sqrt{n}$]에 속하는 소수들을 다 나눠봤을 때, 나눠지는 소수가 하나도 없었다면 n을 소수로 판단
- 오래 걸려서 이 방법만 사용하기는 실용적이지 않다.
- 방법 2: Fermat test
- 다 나눠보는게 아니라, 확률적으로 나눠봄
- p가 소수이고 GCD(a, p) =1이면 $a^{p-1}$ ≡ 1 (mod p)
- GCD(a, p) =1을 만족하는 a에 대해 $a^{p-1}$ ≠ 1 (mod p)이면 p는 소수가 아니다.
- 구하는 방법:
- GCD(a, n) =1인 a를 확률적으로 찾아낸다.
- [$a^{n-1}$ (mod n)]가 1이 아니라면 n이 소수가 아니라는 증가가 된다.
- 방법 3: Miller-Rabin test
- Fermat test와 NSR(Nontrivial Square Root) test를 조합한 방법이다.
- NSR test
- 이론: p가 홀수 소수라면, [$x^2$ (mod p) =1]는 [x = 1, p-1] 이 두 가지 해만 갖는다.
- (1 mod n)의 NSR: [$x^2$ mod n =1]이지만 [x ≠ 1, n-1]인 것
- p가 소수라면 mod p 상에서 1은 trivial square root밖에 가질 수 없다.
- 예: x=4, n=15
- 16 mod 15 = 1이지만, x는 4(Nontrivial Square Root)이다.
- 즉, x는 합성수이다.
- 참고: x mod n에 대해 x가 -1인 것은 x가 n-1인 것과 동일하다.
- 방법 3: Deterministic algorithm
- 확률적이지 않은 정확한 알고리즘
- AKS algorithm이 알려져있다. Trial division보다는 빠르지만 Miller-Robin test보다 비효율적이라 현실적으로 사용하기 어렵다.
- 방법 4: Hybrid
- 주로 사용되는 방법
- 예: Trial division + MR/Fermat
- Trail division 방식으로 몇 개만 나눠보는 것. 몇 개만 나눠봐도 경우의 수를 많이 줄일 수 있다.
- 예를 들어, 2로 나눠봤다면, 모든 정수의 절반으로 범위를 좁힐 수 있다.
Miller-Rabin Algorithm 수도 코드

- 먼저 Miller-Rabin(n, s) 함수부터 보자
- 입력으로 들어오는 n과 s는 다음과 같다.
- n: 소수인지 판별할 정수
- s: test 횟수
- s번 a를 랜덤하게 뽑고 test를 돌린다.
- 입력으로 들어오는 n과 s는 다음과 같다.
- Test(a, n) 함수
- 1 line: [n-1 = $2^tu$]를 성립하는 t와 u를 찾는다.
- 2 line: $x_0$값을 초기화
- 3~5 lines: t만큼 직전 x값에 제곱해가며 값을 구한다.
- 한 번에 계산하지 않고 이렇게 t번에 나눠서 계속 제곱해가는 이유는 NSR test를 진행하기 위함이다.
- 이 for문에서 NSR test를 진행한다. -> 합성수인 증거 찾기
- 7 line: 최종적으로 계산된 x값이 1이 아니면 n이 합성수라고 판단.
- n이 합성수라는 증거를 찾은 것 -> 확실
- 위 Test() 함수를 한 번 돌렸을 때, 오답일 확률(소수 판별)은 1/2이다. 이를 반복하면 오답 확률이 계속 절반으로 줄어들게 된다.
- 즉, 위 Miller-Rabin()함수의 오답률은 1/$2^{s}$이다.
- 구현한 코드:
def miller_rabin(n, s):
if n == 2:
return Prime
elif n % 2 == 0:
return Composite
for _ in range(s):
a = random.randint(1, n-1)
if test(a, n) == True:
return Composite
return Prime
def test(a, n):
t=0
u=n-1 # 하단의 while문에서 u 값이 정해짐
while u%2==0:
t+=1
u/=2
preX=exp(a,int(u),n) # a^u mod n을 구하는 함수 -> 따로 구현 필요
curX=0
for i in range(t):
curX = (preX*preX)%n
if curX==1 and preX!=1 and preX!=n-1:
return True
preX= curX
if curX!=1:
return True
return False
확률적인 알고리즘 종류 2가지
- 입력에 따라 다른 수행시간을 가지는 알고리즘
- 수행 시간은 항상 동일한데, 가끔 틀린 답을 주는 알고리즘
- ex) Miller-Robin algorithm
Miller-Robin test 요약
- 페르마 테스트와 NSR 테스트를 조합한 테스트로 확률적인 알고리즘이다.
- 페르마 테스트
- [$a^{n-1}$ mod n ≠ 1]인 a가 존재하면 n은 합성수이다.
- NSR 테스트
- [$x^2$ mod n =1]일 때, x가 1 또는 -1(n-1)이 아닌 값을 갖는다면 n은 합성수이다.
- 위 두 테스트를 조합한 테스트를 반복하며 오답 확률을 줄인다.
출처:
- [Cryptography and Network Security: Principles and Practices]
반응형
'Computer Security' 카테고리의 다른 글
| [컴퓨터 보안] Classical Encryption Techniques (2) | 2020.10.23 |
|---|---|
| Group, Finite Fields, Polynomial GCD, 다항식을 bit string으로 계산 (0) | 2020.10.23 |
| 역원 구하기 - Euclidean Algorithm / Extended Euclidean Algorithm (0) | 2020.10.22 |
| [컴퓨터 보안] 정수론 기초 - Divisibiliy, GCD, Congruences, Modular, 역원 (2) | 2020.10.22 |
| [컴퓨터 공학] 용어 설명 및 최근 경향 - EPP/EDR/AI (0) | 2020.09.28 |
Comments




