Recent Posts
Link
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 |
Tags
- terminal
- Value too long for column
- 겨울 부산
- 깡돼후
- 코루틴 컨텍스트
- PersistenceContext
- kotlin
- pytest
- preemption #
- PytestPluginManager
- 자원부족
- 티스토리챌린지
- 달인막창
- 코루틴 빌더
- table not found
- tolerated
- k8s #kubernetes #쿠버네티스
- JanusWebRTCGateway
- VARCHAR (1)
- taint
- JanusWebRTCServer
- JanusWebRTC
- Spring Batch
- JanusGateway
- vfr video
- 헥사고날아키텍처 #육각형아키텍처 #유스케이스
- 오블완
- python
- 개성국밥
- mp4fpsmod
Archives
너와 나의 스토리
[Data Mining] CH2. Data (2) 본문
반응형
Similarity and Dissimilarity
- Similarity
- 두 데이터 객체가 얼마나 유사한가 수치적으로 측정
- 객체들이 서로 비슷할수록 값이 큼
- 보통 [0,1] 사이의 숫자를 범위로 사용함
- Dissimilarity (=distance)
- 두 데이터 객체가 얼마나 다른지 수치적으로 측정
- 객체들이 서로 같을수록 값이 작음
- 보통 최소 dissimilarity를 0으로 둠
- 상한(upper limit)은 다름
- Proximity는 similarity와 dissimilarity를 구분하지 않고 사용하는 것
Similarity/Dissimilarity for simple attributes
- p와 q는 두 데이터 객체의 attribute 값

- Nominal은 categorical 타입이라서 순서가 없고, 같다/틀리다만 고려 가능
- 같으면 유사도 높고, 다르면 유사도 낮음 -> 1 or 0
- attribute가 여러개라면 각각 값을 더한다면 attribute 개수로 나누면 된다.
- Ordinal은 순서가 있기 때문에, 정수 [0, n-1] 사이의 숫자로 대응시킨 후, 두 개의 값의 차이를 뺀 것을 (n-1)으로 나눈다.
- (n-1): 가장 거리가 먼 거리 -> (n-1)-0
- Interval or Ratio는 데이터의 개수가 실수이기 때문에 분모를 설정할 수 없음
Euclidean Distance
- Dissimilarity = Distance
- 모든 attribute가 숫자가 됨 -> $P_{k}$: k번째 attribute values 혹은 데이터 벡터
- k=1 -> 첫 번째 attribute

- 만약 스케일이 다르면 standardization 필요함

- p1, p2거리랑 p2, p1거리랑 같으므로 symmetric matrix이다.
Minkowski Distance
- Euclidean Distance를 확장한 것
- n: attribute의 개수, r: 각 attribute 값의 차이의 승

- r=1이면 City block distance라고 함
- 두 이진 벡터 사이에서 다른 bits의 개수
- |x1-x2|+|y1-y2| -> 두 점의 대각선 길이

두 점의 대각선 거리가 최단 거리이기는 하지만 그 네모가 빌딩이라고 생각하면 대각선으로 지나갈 수 없고 오른쪽의 파란색 선처럼 이동해야 함 => city block이라고 불리는 이유
- r=2이면 Euclidean distance
- r->∞이면 "supremum" distance
- 벡터의 컴포넌트들 사이의 최대 거리


Mahalanobis Distance
- p와 q는 n차원 공간의 한 점
- 이 두 점 사이의 거리를 (Euclidean distance)를 일반화한 것
- 아래 그림을 보면, 주성분 분석을 하면 3시 방향으로 데이터가 많이 분포한다(화살표)
- 즉, x라는 attribute와 y라는 attribute의 스케일을 전혀 고려하지 않은 상태의 거리를 구해왔었다
- Mahalanobis Distance는 각 두 선의 거리를 같은 거리가 되게끔 스케일링을 해준다.
- 즉, 저 데이터들의 분포가 원처럼 보이게 됨.


- 실제로는 AC 길이가 훨씬 멀지만, 스케일링을 거치면 ↗방향 데이터 분포 비율로 따지면 별로 긴 거리가 아니여서 Mahalanobis distance는 AB가 더 크다.
Distance에 대한 공통 특징
- 보통 Distance가 metric 특성을 만족하도록 정의한다. -> 꼭 만족하지는 않아도 됨
- 만족시키면 search할 때 좋음
- Euclidean distance같은 거리들은 다음과 같은 특성을 가진다.
- d(p,q) ≥ 0 for all p and q && d(p,q)=0 only if p =q (Positive definiteness)
- 두 점 사이의 거리가 양수이여야 한다.
- 두 점 사이의 거리가 0이려면 두 점이 반드시 같아야한다.
- d(p,q) = d(p,q) for all p and q (Symmetry)
- d(p,r) ≤ d(p,q)+d(q,r) for all points p, q, and r. (Triangle Inequality)
- 삼각형 세 점을 각각 p,q,r로 잡고 생각하면 됨
- d(p,q) ≥ 0 for all p and q && d(p,q)=0 only if p =q (Positive definiteness)
- 위 1~3을 만족하는 distance는 metric property를 만족한다고한다.
Similarity의 공통 특성
- similarity 공통 특성:
- s(p,q)=1 (or maximum similarity) only if p=q
- s(p,q)=s(q,p) for all p and q. (Symmetry)
- s(p,q): 점들(데이터 객체들) 사이의 similarity
Similarity between binary vectors
- 일반적인 상황은 데이터 객체 p,q가 binary attributes만 가지는 것이다.
- binary attribute: 0 또는 1만 가짐
- 다음과 같은 양에 따라 유사도 연산

- $M_{00}$, $M_{11}$ -> 두 개 같은 값
Simple Matching and Jaccard Coerricients
- Simple Matching: 일치하는 것 / 전체
- Jaccard Coerricients: ex) 피 검사할 때, 음성인지 양성인지 판단할 때, 두 사람이 양성으로 일치하는지만 확인하고 음성인지 확인할 필요는 없으므로 $M_{00}$을 분모, 분자에서 모두 삭제
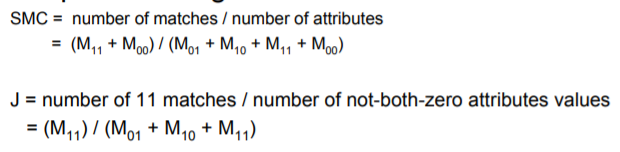

Cosine Similarity
- 만약 d1, d2가 두 개의 document vectors이러면,
- cos(d1, d2) = (d1●d2)/ ||d1|| ||d2|| (●: 벡터 곱)
- cos 0 = 1, cos 90 = 0, cos 180 = -1
- 즉, d1, d2 두 벡터 사이의 각이 0이라는 것은 방향이 같다는 것 => 유사도가 가장 높다
- 즉, 벡터의 크기보다는 벡터 사이의 각이 중요하다!

Extended Jaccard Coefficient (Tanimoto)
- binary가 아니라 continuous(연속적, 무한) or count(유한한) attributes를 위한 Jaccard 변형

Correlation
- 객체 사이의 선형 관계 측정
- 상관관계를 연산하기 위해서 우리는 데이터 객체를 표준화(standardize)한 후, 점곱을 취한다.

Combining Similarties를 위한 일반적인 접근
- Attribute는 서로 다른 타입을 가질 수도 있지만 전반적인 유사도는 필요하다

Combine Similarites를 위한 가중치 사용
- 모든 attributes를 똑같이 취급하기 싫을 수 있다.
- [0, 1] 사이의 값을 가지고, 합이 1이 되는 가중치($W_{k}$)를 사용할 수 있다.

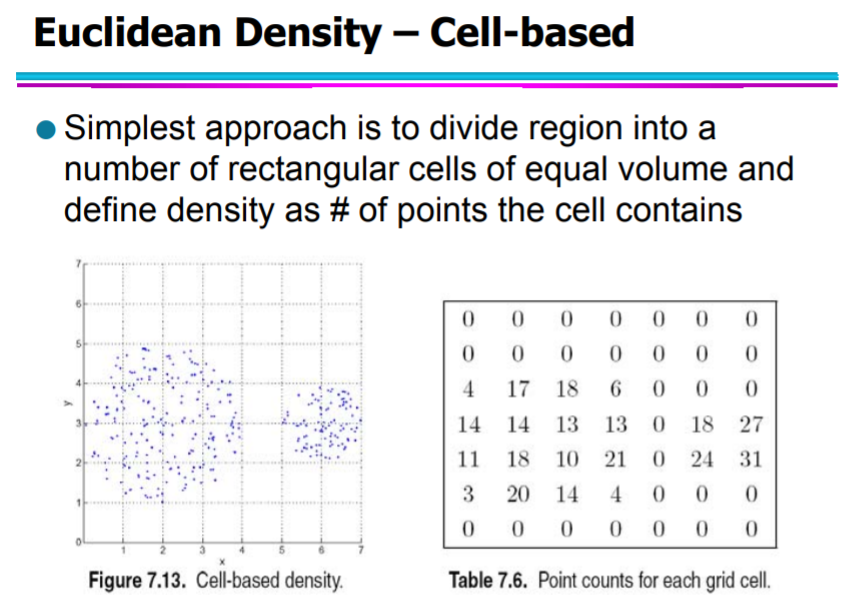
Density
- Density-based clustering: 밀도 기반으로 데이터 묶기 -> density에 대한 notion 필요
- Examles:df
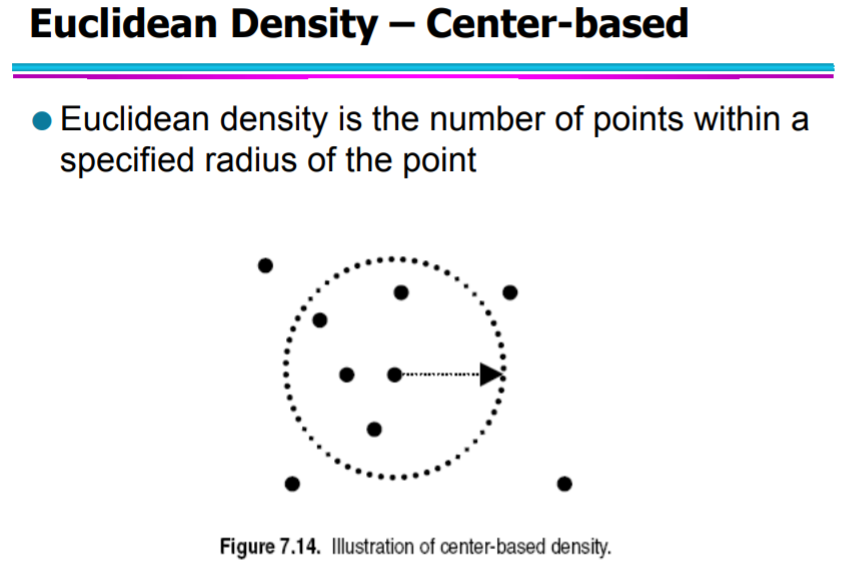
- Euclidean density ( = 단위 부피 당 점들의 수 )
- Probability density
- Graph-based density
반응형
'Data Analysis > Data Mining' 카테고리의 다른 글
| [Data Mining] Ch4. Classification: Basic concepts, Decision trees, and Model evaluation (2) (0) | 2020.04.07 |
|---|---|
| [Data Mining] Ch4. Classification: Basic concepts, Decision trees, and Model evaluation (1) (0) | 2020.04.04 |
| [Data Mining] CH3. Data Exploration (2) (0) | 2020.03.31 |
| [Data Mining] CH3. Data Exploration (1) (2) | 2020.03.25 |
| [Data Mining] CH2. Data (1) (2) | 2020.03.21 |
Comments




