Recent Posts
Link
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |||
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 |
Tags
- pytest
- Value too long for column
- 자원부족
- 오블완
- vfr video
- preemption #
- 코루틴 컨텍스트
- terminal
- 겨울 부산
- JanusGateway
- JanusWebRTC
- Spring Batch
- VARCHAR (1)
- k8s #kubernetes #쿠버네티스
- JanusWebRTCGateway
- 달인막창
- PersistenceContext
- taint
- 코루틴 빌더
- 개성국밥
- 깡돼후
- kotlin
- tolerated
- 티스토리챌린지
- JanusWebRTCServer
- 헥사고날아키텍처 #육각형아키텍처 #유스케이스
- table not found
- PytestPluginManager
- python
- mp4fpsmod
Archives
너와 나의 스토리
[Data Mining] Ch4. Classification: Basic concepts, Decision trees, and Model evaluation (2) 본문
Data Analysis/Data Mining
[Data Mining] Ch4. Classification: Basic concepts, Decision trees, and Model evaluation (2)
노는게제일좋아! 2020. 4. 7. 15:19반응형
Gini Index (IBM intelligent miner)
- 어떤 노드에 대응되는 트레이닝 데이터의 불순도의 정도를 측정하는 지표
- 이 값이 크면 불순도가 큰 것. 즉, 이 값이 작을수록 분류를 잘했다고 판단 가능


- [부모의 gini index(=$gini(T)$)]과 [자식의 gini index(=$gini_{split}(T)$) 차이가 클수록 좋은 것
- 잘 split 한 것

- gain이 최대가 되는 split이 최적의 split

- Gini 값은 낮을 수록, Gain은 높을수록 좋다.

- Gini(N1) = 1- $\sum_{j=1}^{클래스 개수}(\frac{N1의 C1 개수}{N의 C1 개수})^2$

- 첫 번째 split의 Gini 값이 가장 작으므로, 이렇게 split하는 것이 좋다
Continuous Attributes: Computing Gini Index
- continuous한 경우에는 distinct values의 값이 너무 많다 => 가능한 child의 개수가 너무 많음
- Binary로 제한해서 값을 나눠보자
- A < v and A ≥ v 로 나누자
- v는 다 대입해보고 gini 값이 낮은 것으로 선택하자
- => 비효율적인 연산 (반복 연산이 너무 많음)
- 효율적인 연산을 위해, 각 attribute에 대해
- attribute 값 정렬
- v값을 경계 값들로 선택 (회색)
- 각 v에 대해 Gini 값 구하기

Splitting based on Information Gain
- Information Gain = $Entropy(p) - \sum_{i=1}^{k}\frac{n_i}{n}Entropy(i)$
- Information Gain이 클수록 좋다고 앞서 말했었다
- ID3 와 C4.5 사용
- 단점: 여러개로 나눠지는 경우(값의 개수가 많은 attribute)에 (IG)결과가 더 좋게 나오는 경향이 있다.
- 예를 들어, age가 더 좋음에도 불구하고, name의 총 Entropy가 더 작다.
- 하지만, name으로 나누는건 의미 없다.

- 이런 단점을 보안한 것이 gain ratio이며, C4.5에서 사용한다.
- GainRatio(A) = InfoGain(A)/SplitInfo(A)
- 최대 gain ratio를 보이는 Attribute를 선택

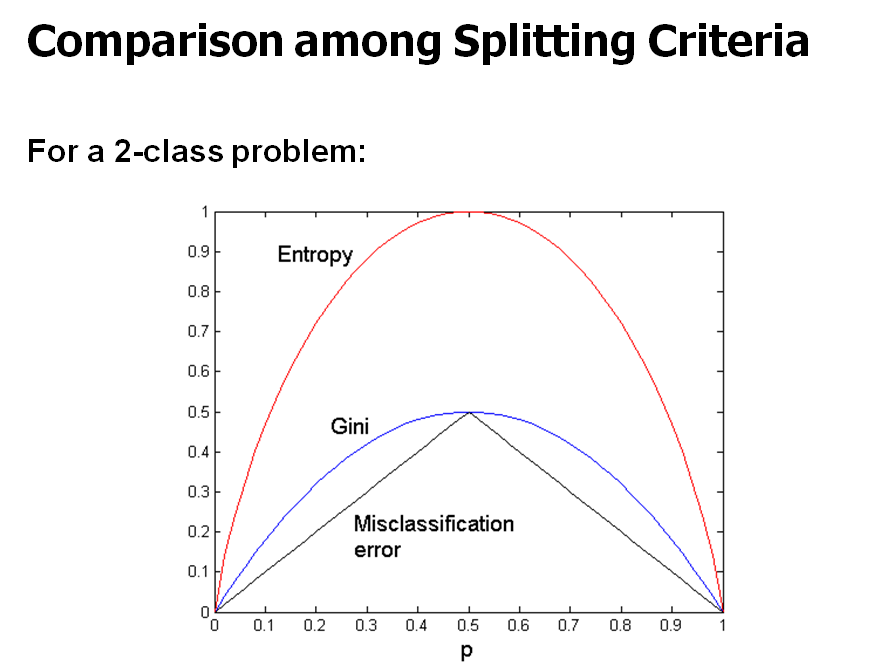
Splitting criteria based on Classification Error
- 노드 t의 classification error:
- Error(t) = 1 - $max_{i}P(i|t)$
- 노드 t에 있는 i번째 class의 상대빈도 중에서 제일 큰 것을 1에서 빼준 것
- 노드 t에 있는 classes들의 개수를 보고 노드의 class를 판단하는데,
- 노드의 class를 합리적으로 판단하는 법: 그 노드에 대응되는 트레이닝 데이터 중에서 제일 많이 들어들어 있는 클래스로 그 노드의 분류(split)를 정하는 것이 합리적이다.
- $max_{i}P(i|t)$: 정확도

Decision Tree Algorithm
- 기본 알고리즘 (greedy algorithm)
- top-down recursive divide-and-conquer manner
- greedy algorithm: 데이터를 쭉 스캔하면서 순간 순간 최적이락 생각되는 것을 선택해 나가는 방식
- 시작시, 모든 훈련데이터를 tree의 root에 놓는다.
- 특정 기준(IG)에 의해 테스트 attribute를 선택하고 자식 노드들을 생성한다
- attribute 값에 따라 자식 노드들에 훈련 데이터를 분배한다.
- 위 작업을 재귀적으로 중단 조건이 만족될 때까지 반복한다.
- IG가 최대가 되는 attribute 선택
- 중단 조건
- 노드의 모든 데이터의 class label이 모두 같은 경우
- 분할에 사용될 test attribute 또는 training data가 더 이상 없다
- 다수결 투표(majority voting)로 class label을 결정
- 부모 노드의 트레이닝 데이터의 다수결 투표에 의해 class label 결정
- 다수결 투표(majority voting)로 class label을 결정
- 장점
- cost가 작음 -> 모델 만드는 시간이 빠름
- unkown records를 분류하는 속도가 빠름
- tree 이해하기 쉬움 -> 왜 그렇게 분류했는지
- 다른 분류 기술들에 비해 상대적으로 정확도가 높음
Practical Issues of Classification
- Underfitting and Overfitting
- overfitting: 너무 트레이닝 데이터에 최적화해서 테스트 데이터에 대해 성능이 떨어짐
- Missing Values: 특정 attribute에 값이 안 들어간 경우
- 값이 없어서 안들어가는 경우
- 값을 모르거나 의도적으로 값을 입력 안한 경우
- Costs of Classification
Underfitting and Overfitting
- Underfitting
- 모델이 너무 단순해서 데이터의 내재된 구조를 학습하지 못할 때 일어남
- 아래 그래프의 초반 부분
- Overfitting
- decision tree를 필요 이상으로 복잡하게 만듦으로써 오는 결과
- node 개수가 많다는 것 = tree가 복잡한 형태 -> 트레이닝 데이터에 대한 error는 적음
- tree가 어느정도 복잡해지면 오히려 test data는 분류 잘 못 함

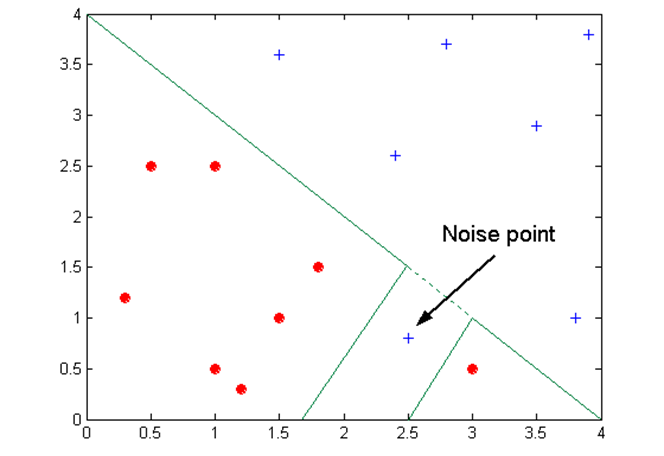
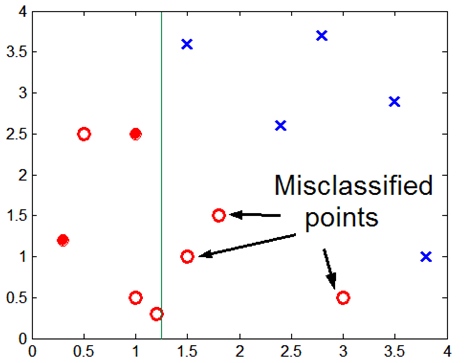
- Overfitting 발생하는 이유:
- Noise 때문에
- 불충분한 데이터 때문에
Occam's Razor
- "어떤 것을 설명하는데는 가장 단순한 가정으로부터 시작해야한다"
- 유사한 일반화 오류(모델의 실제 에러->test data로 측정)의 두 모델을 고려할 때, 더 복잡한 모델보다 더 단순한 모들을 선호해야 한다.
- 트레이닝 데이터에 너무 적합하게 만들어서 모델이 복잡한 걸 수도 있다.
- 그러므로, 모델을 평가할 때, 모델의 복잡성을 평가해서 평가해야한다.
모델 평가
- Performance 평가를 위한 지표(Metrics)
- 모델의 performance를 어떻게 평가할 것인가
- Performace 평가 방법
- 어떻게 믿을만한 평가를 할 수 있을까?
- 모델 비교 방법
- 어떻게 모델들의 performance를 상대적으로 비교할 수 있을까?
Metrics for performance evaluation
- "모델을 얼마나 빨리 만드느냐?" / "얼마나 빨리 분류를 하느냐?" / "데이터에 따른 성능 비교" 이런 것 보다는
- 모델이 얼마나 정확하게 분류하는지 평가해보자
- Confusion Matrix:

- Accuracy의 한계
- binary classification(2-class)에서 문제
- ex) [class0 examples = 9990 / class1 examples = 10]
- 만약 모델이 모든 것을 class0으로 예측(분류)한다면, 정확도는 9990/10000 = 99.9%
- binary classification(2-class)에서 문제
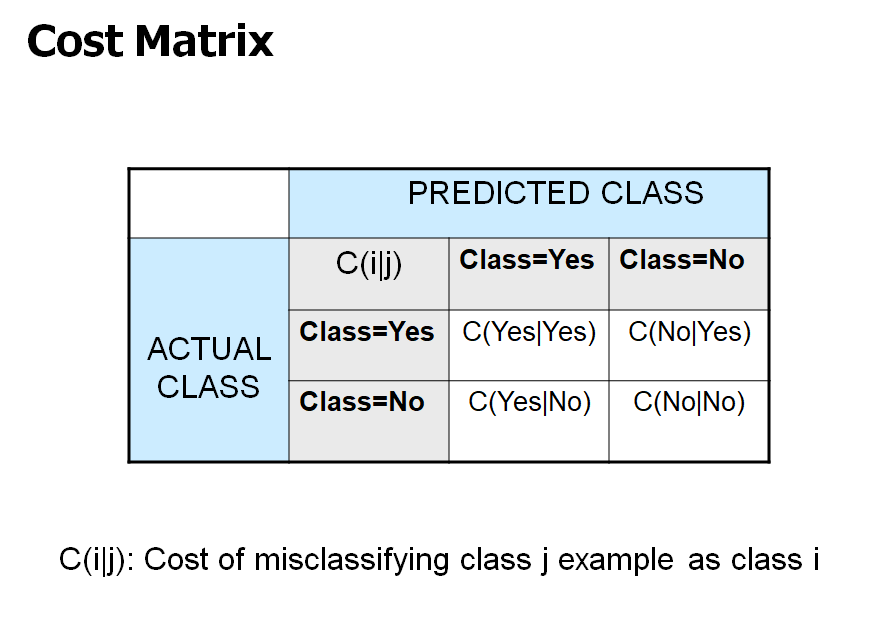
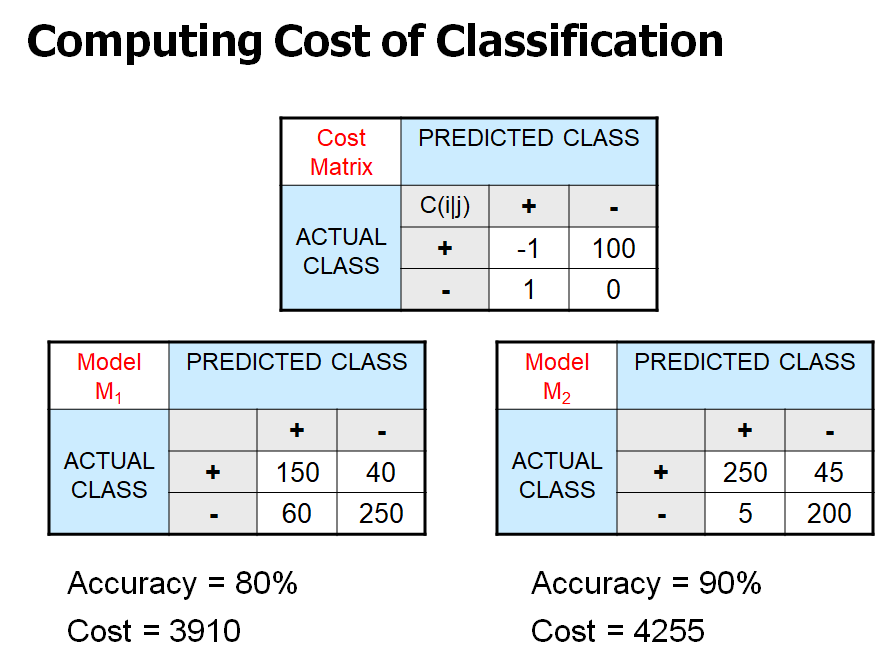
- Cost Matrix
- [i = +]: 암 환자 / [i = -]: 정상 환자
- [j = +]: 암이라고 진단 / [j = -]: 정상이라고 진단
- 암 환자를 정상이라고 진단하면 병원은 손해 배상을 해야 함 -> cost가 큼
- 암 환자를 암이라고 진단하면 병원은 병원비를 받음 -> minus cost
- 정상 환자를 암이라고 진단하면 가벼운 사과로 해결 가능 -> cost 작음
- 정상 환자를 정상이라고 진단하면 아무일도 일어나지 않음 -> cost = 0
- 즉, 1번과 3번 모두 오진이지만, cost가 다름
- M2 모델이 M1보다 정확도는 높지만, cost 기준으로는 M1이 더 낮기 때문에 좋은 모델로 볼 수 있다.
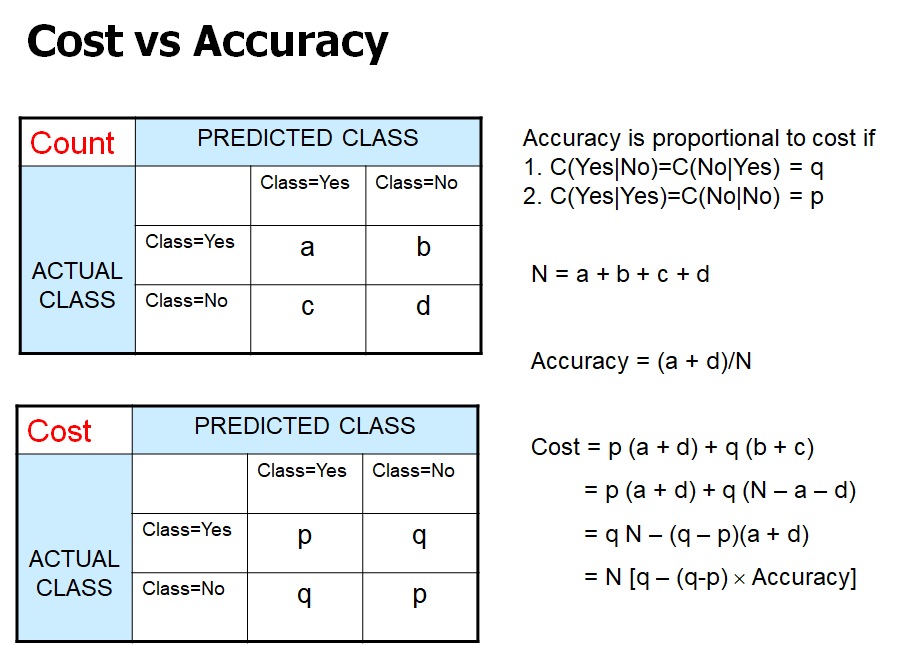

- Precision(p): 의사가 분류한 것의 정확도
- Recall(r): 환자 중에 몇 %나 환자로 잘 판단했는가
- a: TP / b: TF / c: FT / d: FF
반응형
'Data Analysis > Data Mining' 카테고리의 다른 글
| [Data Mining] Ch5. Alternative Classification (0) | 2020.04.15 |
|---|---|
| [Data Mining] Ch4. Classification: Basic concepts, Decision trees, and Model evaluation (3) (0) | 2020.04.15 |
| [Data Mining] Ch4. Classification: Basic concepts, Decision trees, and Model evaluation (1) (0) | 2020.04.04 |
| [Data Mining] CH3. Data Exploration (2) (0) | 2020.03.31 |
| [Data Mining] CH3. Data Exploration (1) (2) | 2020.03.25 |
Comments




